Expliquer l'harmonie en musique

Cette note traite des origines de l'harmonie en théorie de la musique occidentale, de Pythagore à Bill Withers ;)
Nos instruments ont 12 notes. Pourquoi ? Comment se combinent-elles ? Quels sont leurs liens harmoniques ?
Objectif:
Les réponses à ces questions ont pour but de :
- se situer dans l’ensemble des combinaisons et des transitions possibles avec ces 12 notes
- faciliter l’apprentissage d’un morceau, en identifiant les notes, les accords, les combinaisons et les transitions connues
- ouvrir des possibilités de jeu en dehors des théories classiques (modes, tonalités …)
- acquérir des repères afin d’utiliser au mieux le temps passé à la pratique d’un instrument
Plan:
Entrechoquons deux objets, ils vibrent et produisent un son. Partons de cette observation physique pour :
- reconstruire les notions couramment utilisées en musique : note, intervalles, gammes, modes, tonalités, degrés, formes, etc.
- visualiser ces notions sur le clavier d’un piano.
- explorer la construction de gammes et le choix de notes en fonction de leurs relations harmoniques, de la consonance à la dissonance.
C’est parti :
La perception d’une vibration
L’Histoire attribue à Pythagore la construction d’une gamme de notes en partant de l’observation d’une corde pincée, en vibration.
Un corps en mouvement vibre et fait vibrer le milieu (l’air, l’eau …) dans lequel il se trouve. Cette vibration se propage mécaniquement jusqu’à notre oreille. A ce stade, la perception du phénomène en tant que ‘son’ dépend donc essentiellement du milieu de propagation et de la physiologie de notre organe sensoriel. Quand le cerveau commence à interpréter le message sensoriel on parle d’ouïe.
Ce sens est capable de discerner une oscillation principale et un ensemble d’oscillations régulières. En physique il s’agit d’une fréquence fondamentale et de fréquences harmoniques. Une corde de guitare pincée, par exemple, produit une fréquence fondamentale et ses harmoniques. Un son sans fréquence fondamentale est un bruit. La fréquence fondamentale permet d’identifier une note de musique. L’ensemble combiné des fréquences produites par un corps en vibration correspond à son timbre (ce sera celui de l’instrument en musique). Illustration du timbre :
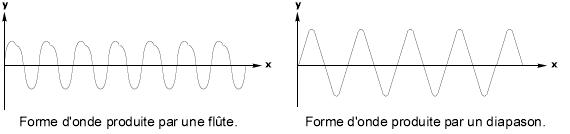
La consonance
Dans un sens la consonance et la dissonance sont des notions culturelles. Les habitudes rendent certains sons plus agréables que d’autres. Si avec nos instruments occidentaux on remarque des dissonances, le ‘jouer faux’ devient relatif lorsque certaines musiques amènent progressivement des accords qui seraient perçus dissonants en début de composition. L’Histoire nous a habitué, en occident, aux consonances issues des mathématiques que voici.
Les fréquences multiples d’une puissance de 2 d’une fréquence fondamentale sont appelées ses harmoniques pures. A l’oreille, une fréquence fondamentale et ses harmoniques pures sont parfaitement consonantes (elles donneront l’intervalle d’octave). Les fréquences multiples d’un entier d’une fondamentale sont ses harmoniques naturelles.
La consonance correspond à des rapports de fréquences de quotient simple, autrement dit lorsque le facteur de multiplication ou de division est un facteur premier petit. Autrement dit, plus le ppcm (Plus Petit Commun Multiple) des deux fréquences est petit, plus elles sont consonantes. Illustration de ces rapports simples :
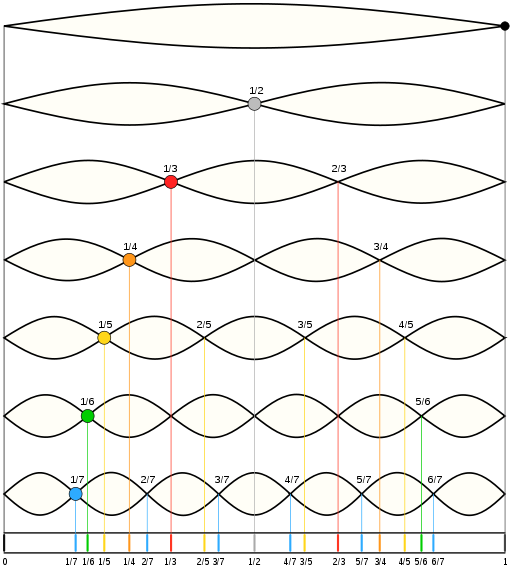
Construisons des gammes
C’est ici qu’intervient Pythagore, cité plus haut. Reprenons l’idée de la corde pincée. Les fréquences d’une gamme peuvent s’obtenir par des diminutions successives de la longueur de corde. Diminuer la longueur de corde augment la fréquence de la fondamentale d’autant.
La gamme d’octaves
En utilisant des diminutions de 1/2 de la longueur de corde, en restant dans les limites du spectre des fréquences audibles par l’être humain (environ de 50 Hz à 18000 Hz), pour une première corde vibrant à 55 Hz, nous ne pourrons obtenir qu’une seule gamme de seulement 9 notes :
55Hz,110Hz,220Hz,440Hz,880Hz,1760Hz,3520Hz,7040Hz,14080Hz.
Elles seront perçues “parfaitement consonantes”, mais probablement aussi limitées en expression.
La gamme pythagoricienne
Elle adopte ces deux choix : utiliser un rapport de 3/2 pour générer la gamme, se limiter à 12 notes. (remarque sur le premier choix : sur certains instruments hindous c’est 24 note) Avec le nouveau rapport on obtient bien plus de fréquences qu’au paragraphe précédent :
55Hz,82.5Hz,123.75Hz,185.625Hz, etc
Il est possible d’utiliser la consonance parfaite (multiplier ou diviser les fréquences par 2), plusieurs fois s’il le faut, pour transposer chacune de ces fréquences entre la fréquence de départ (55Hz) et son double (110Hz) à consonance parfaite. Par exemple : entre 55 et 110 Hz il est possible de replacer 185.625 / 2 = 92.81 Hz. Il faut effectuer cela 12 fois pour créer la gamme nommée Pythagoricienne.
Cette gamme est donc obtenue en multipliant jusqu’à 12 fois par 3/2 une fréquence donnée, et en divisant chacune des 12 fréquences obtenues par la puissance de 2 suffisamment grande pour que le résultat soit compris entre la fréquence donnée initialement et son double. Dans la limite du spectre des fréquences audibles, il est possible d’obtenir 9 groupes complets de 12 fréquences.
Remarque : par le jeu des puissances de 2, chacune des fréquences d’un groupe est donc parfaitement consonante avec la fréquence de même rang des 8 autres groupes. Autrement dit, les premières fréquences de chaque groupe sont parfaitement consonantes (fréquences harmoniques pures de facteur 2 ou 1/2), de même pour les deuxièmes, etc … Ces liens seront utilisés pour désigner des octaves.
Voici les fréquences de la gamme pythagoricienne obtenue à partir d’une fréquence initiale (une corde qui vibre) choisie à 440 Hz. Cette référence donne le ‘La’ et ces fréquences seront utilisées pour désigner nos notes de musique. La notation anglaise est utilisée ( LA= A, SI= B, DO= C, RE= D, MI= E, FA= F, SOL= G ) :
A 440Hz * 3/2
= E 660Hz * 3/2
= B 990Hz * 3/2
= F# 1485Hz * 3/2
= C# 2227Hz * 3/2
= G# 3341Hz * 3/2
= D# 5011Hz * 3/2
= A# 7516Hz * 3/2
= F 11274Hz * 3/2
= C 16911Hz * 3/2
= G 25366Hz * 3/2
= D 38049Hz * 3/2
Pour l’instant la gamme qui vient d'être calculée se trouve classée par ordre de génération. Diviser ces fréquences par la puissance de 2 suffisante afin de ramener toutes ces fréquences dans le spectre audible et entre le LA 440 Hz et son double à consonance parfaite le LA 880 Hz :
A 440Hz
E 660Hz
B 990Hz / 2 = 495 Hz
F# 1485Hz / 2 = 742 Hz
C# 2227Hz / 4 = 556 Hz
G# 3341Hz / 4 = 435 Hz
D# 5011Hz / 8 = 626 Hz
A# 7516Hz / 16 = 469 Hz
F 11274Hz / 16 = 704 Hz
C 16911Hz / 32 = 528 Hz
G 25366Hz / 32 = 792 Hz
D 38049Hz / 64 = 594 Hz
Sur un instrument ou une partition, les notes seront posées dans l’ordre croissant des fréquences.
1. A 440 Hz
2. A# 469 Hz
3. B 495 Hz
4. C 528 Hz
5. C# 556 Hz
6. D 594 Hz
7. D# 626 Hz
8. E 660 Hz
9. F 704 Hz
10. F# 742 Hz
11. G 792 Hz
12. G# 835 Hz
La même gamme se retrouve plus haut en fréquence. Ce sera l’octave supérieure.
1. A 880 Hz
2. A# 938 Hz
3. B 990 Hz
4. C 1056 Hz
5. C# 1112 Hz
6. D 1188 Hz
7. D# 1272 Hz
8. E 1320 Hz
9. F 1408 Hz
10. F# 1484 Hz
11. G 1584 Hz
12. G# 1670 Hz
Voici la gamme triée pas ordre de fréquence à partir de C : C C# D D# E F F# G G# A A# B
Voici la gamme triée par ordre de génération à partir de C : C G D A E B F# C# G# D# A# F
Sur un piano, les notes sont triées par ordre croissant de fréquence, mais les touches blanches et les touches noires regroupent les notes de génération proche.
La gamme tempérée, cycles et intervalles réguliers
La gamme tempérée est celle utilisée aujourd’hui en musique occidentale. Elle peut se définir par rapport à la gamme pythagoricienne.
Si l’on poursuit la génération de la gamme pythagoricienne, le calcul d’une N ème fréquence (au delà de 12) ne permet pas d’obtenir un multiple exact de celle initialement donnée. L’écart entre la 12ème fréquence et la fréquence double de celle initialement donnée n’est pas le même qu’entre les 12 autres fréquences. Cette irrégularité fait qu’un même intervalle n’aura pas forcément le même degré de consonance, selon l’endroit ou il est pris : dans une même octave ou à cheval sur deux octaves. Par exemple : l’écart entre le SOL d’une octave et le DO de l’octave supérieure ( 5 notes d’écart ), ne sonne par pareil que l’écart entre le DO et le FA d’une même octave (pourtant 5 notes d’écart aussi).
Afin de lisser ce problème, la gamme dite tempérée, est créée en divisant en 12 parties équivalentes l’écart entre une fréquence et son double (parfaitement consonant). Les fréquences obtenues correspondent à peu de chose près à celle obtenue pour la gamme pythagoricienne, au point qu’il est très difficile d’entendre la différence (l’humain distingue une différence de 1Hz au maximum, comme pour le décibel l’unité a été choisie pour cette raison).
Les 9 groupes de 12 fréquences sont perçus avec les mêmes consonances que pour la gamme pythagoricienne, mais les fréquences sont espacées de manière identiques sur l’échelle logarithmique des fréquences. Par rapport à la pythagoricienne, les écart de fréquence étant réguliers, sur cette gamme, les notes s’enchainent maintenant de manière cyclique.
La gamme naturelle
Elle nous sert à comprendre la notion de consonance et de dissonance. On découvre la génération des accords dits ‘parfaits’. La gamme naturelle est générée par la suite des multiples entiers d’une fréquence fondamentale (d’un corps en vibration). Pour un Do (C) à 528 Hz , les harmoniques naturelles sont donc :
1. 528 Hz => C
2. 1056 Hz /2 = 528
3. 1584 Hz /2 = 792 => G
4. 2112 Hz /4 = 528
5. 2640 Hz /4 = 660 => E
6. 3168 Hz /4 = 792
7. 3696 Hz /4 = 924 => ~A#
8. 4224 Hz /8 = 528
9. 4752 Hz /8 = 594 => D
10. 5280 Hz /8 = 660
11. 5808 Hz /8 = 726 => entre F et F#
12. 6336 Hz /8 = 792
13. 6864 Hz /8 = 858 => entre G# et A
14. 7392 Hz /8 = 924
15. 7920 Hz /8 = 990 => B
16. 8448 Hz /16= 528
17 561 => ~C#
18 594
19 627 => ~D#
20 660
21 693 => ~F
22 726
23 759 => ~F#
24 792
25 825 => ~G#
...
La première colonne de fréquences correspond aux multiples de la fondamentales (harmoniques pures). Dans la deuxième colonne, les fréquence ont été divisées par une puissance de 2 (gardant la consonance parfaite) suffisamment grande pour que le résultat soit situé entre la fondamentale et son double. En troisième colonne, le rapprochement des fréquences est fait avec la gamme tempérée, dont on reconnait les notes. On observe ainsi la formation de l’accord dit ‘parfait’, “DO(C),SOL(G),MI(E)”, qui correspondant à une fondamentale et ses deux premières harmoniques naturelles.
Pour un LA 440 Hz, les harmoniques sont :
1. 440 Hz => A
2. 880 Hz /2 = 440
3. 1320 Hz /2 = 660 => E
4. 1760 Hz /2 = 880
5. 2200 Hz /4 = 550 => C#
6. 2640 Hz /4 = 660
7. 3080 Hz /4 = 770 => G
8. 3520 Hz /4 = 880
9. 3960 Hz /8 = 495 => B
10. 4400 Hz /8 = 550
11. 4840 Hz /8 = 605 => D
12. 5280 Hz /8 = 660
13. 5720 Hz /8 = 715 => ~F
14. 6160 Hz /8 = 770
15. 6600 Hz /8 = 825 => ~G#
16. 7040 Hz /16 = 440
17. 7480 Hz /16 = 467 => #A#
...
L’accord dit ‘parfait’ reconnu ici est “LA (A), DO# (C#), MI (E)”.
L’harmonie
En musique les notes sont jouées successivement et/ou simultanément. Les timbres de différents instruments se suivent et se mélangent En physique une analyse spectrale 1 de la musique permet de ‘décomposer’ (de retrouver) les fréquences. L’harmonie, dans la théorie de la musique occidentale, consiste à jouer avec le degré de consonance entre les note.
Le jeux consiste à savoir où l’on est, d’où l’on vient, et où on veut aller. Pour cela une carte serait bien pratique. Cette carte serait une représentation graphique des gammes construites précédemment. Elle mettrait en évidence les degrés de consonance entre les notes. Sur la gamme tempérée, la mise en évidence des consonances peut se faire par le recoupement avec la gamme naturelle. Cela permet de classer les fréquences par ordre de consonance. La gamme tempérée étant cyclique, le degré de consonance de deux notes dépend de leur écart, quelque soit la position des deux notes dans dans le cycle.
Autrement dit, parce que la gamme tempérée est cyclique, les écarts permettent de connaitre le degré de consonance entre n’importe quelle couple de notes. Par exemple, la génération de la gamme naturelle à partir de C a permis un recoupement (par identification et rapprochement des fréquences) avec la gamme tempérée. Voici la gamme par ordre de consonance :
C G E (~A#) D (F/F#) (G#/A) B (~C#) (~D#) (~F) (~F#) (~G#) A ?
Voici la position de ces notes dans la gamme classée en ordre croissant de fréquence ( “C C# D D# E F F# G G# A A# B” ) :
entre C et
G : 7 notes
E : 4 notes
(~A#) : 10 notes
D : 2 note
(F/F#) : 5/6 notes
(G#/A) : 8/9 notes
B : 11 notes
(~C#) : 0
(~D#) : 2
(~F) : 4
(~F#) : 5
(~G#) : 7
A ? : 8
Pour une note donnée sur la gamme tempérée classée par ordre croissant de fréquences, la plus consonante sera la 7ème (écart de 6 notes), puis la 4 ème (écart de 3 notes) le sera un peu moins, ainsi de suite …
Les deux premiers écarts (les plus consonants, donc) correspondent à ceux donnés habituellement en musique occidentale pour l’accord parfait “C(DO) E(MI) G(SOL)”. Ces deux écarts sont appelés intervalles de tierce et de quinte.
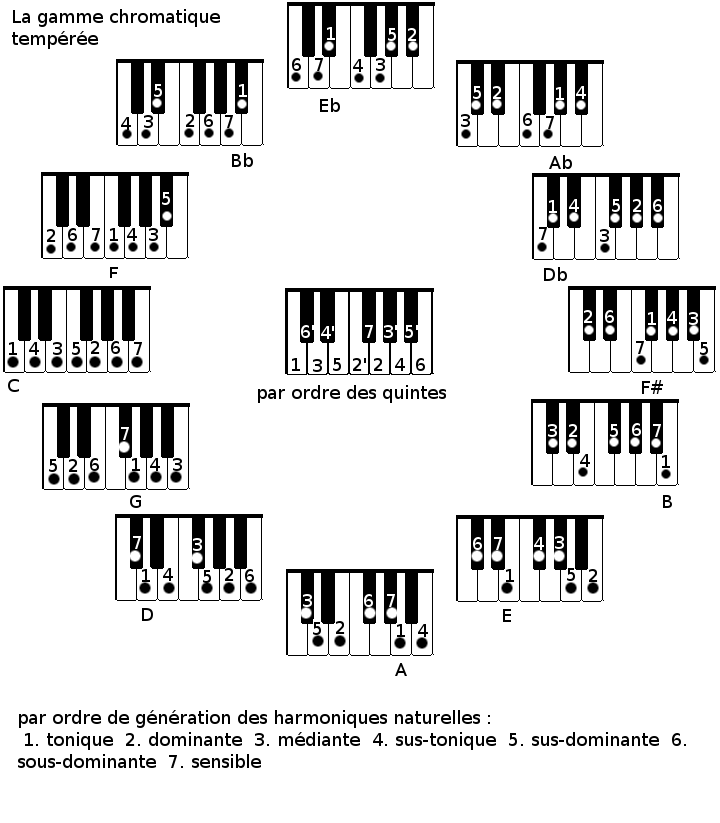
Cette carte reprend une partie des observations de consonance effectuées jusque là sur les gammes pythagoricienne et naturelle. Cette carte n’est pas une vision exhaustive des harmonies possibles, qui seraient plutôt du ressort d’une analyse spectrale. C’est un bon moyen de se repérer en musique occidentale, et par rapport aux consonances observées par les constructions pythagoriciennes et naturelles de la gamme tempérée.
Question sur la composition
Sur la “carte” présentée ci-dessus, il y a 7 (notes) * 12 (games) = 84 positions de départ possibles pour une première note. Le dénombrement est pour l’instant simple.
Pour le choix d’une deuxième note, en fonction du degré de consonance, plus la note ajoutée sera éloignée de la note de départ (dans la gamme triée par ordre de consonance), moins l’ensemble sera consonant. Pour le choix de la note suivante : la consonance du résultat dépend des écarts entre cette nouvelle note et chacune des notes précédentes. Ainsi de suite …
Choisir des notes ainsi, c’est construire une mélodie ou un premier accord. Choisir un deuxième accord, c’est garder les notes communes, enlever des notes, et en ajouter d’autres. Le degré de consonance des deux accords dépend du degré de consonance entre chaque notes du premier et du deuxième accord. Le dénombrement des possibilités a largement grandit.
Dans l’absolu n’importe quelle note ou groupe de note peut succéder à n’importe quelle autre. Le choix de cette représentation cartographiée par les gammes diatoniques permet un repérage. Si l’on dépasse les 12 notes dans la construction de la gamme (tempérée, occidentale) le choix tend vers l’infini est le repérage s’approche du domaine de l’analyse spectrale. Le choix d’une gamme à 12 notes est-il suffisant pour s’exprimer (gamme indienne à 64 notes) ?
Que faire ?
Jouer. Se repérer. Expérimenter des chemins sur cette carte. S’exprimer. Augmenter son vocabulaire.
J’apprécie la méthode de Jamey Aebersold 2 : essayer de jouer directement d’oreille vos morceaux préférés, le faire en partant de n’importe quelle note, découvrir, après coup, sur la partition originale, ce que l’auteur a écrit.
Pour apprendre à jouer d’un instrument il est bon d’essayer de jouer d’oreille une oeuvre que vous aimez. Par le jeu il faut chercher à identifier les éléments qui composent l’oeuvre. Le choix de l’oeuvre est essentiel. Dans l’absolu le nombre et la variété des oeuvres étudiées augmente l’expérience, mais il faut choisir une oeuvre à la fois accessible et interessante à son niveau. C’est le rôle de l’enseignant : connaître les chemins, connaître ses élèves, aider l'élève dans ses choix. Cette exploration permet notamment d’identifier les notes, les intervalles, les accords, les progressions d’accords, et les modulations. Midi Chord Display aide à identifier l’harmonie soi-même, en nommant les accords.
Quid des partitions ? Elles permettent de découvrir l’harmonie d’une oeuvre telle que son compositeur l’a écrite. On découvre beaucoup en étudiant les partitions originales. De nombreuses sources de partitions et de tablatures existent. 3 Vous pouvez aussi obtenir les accords d’un oeuvre par analyse spectrale, en envoyant le fichier audio sur un site. 4
Quid du solfège ? La lecture et l'écriture sont des moyens d'échange, de communication. Quid des notations utilisées ? On finit par être polyglote, les notations françaises et anglosaxones sont souvent mélangées. Il est possible de tout lire. Les grilles d’accord sont un bon début, les ‘RealBooks’ notamment 5
Jouer d’un instrument permet de découvrir des parcours (sur la carte) connus et nommés (le vocabulaire du musicien). Les plus utilisés sont :
- la gamme chromatique qui désigne l’enchaînement des 12 notes. Elle tire son nom du fait qu’elle contient toutes les notes (couleurs) existantes.
- la gamme diatonique est un sous ensemble de la gamme chromatique, ne désignant que 7 notes, obtenue en ne prenant que les 2,4,5,7,9 et 11ème notes après une note donnée sur la gamme chromatique.
remarques : ce sont les premières notes de la gamme naturelle générée pour une note donnée, et donc les plus consonantes (pour rappel, aux rapports de fréquences les plus simples) En partant de DO (C), ce sont toutes les touches blanches d’un piano. Sur cet exemple des touches blanches qui donne la gamme diatonique de Do, on remarque que la 3ème note (le Mi) suit la quatrième (le Fa) et que la 7ème note (le Si) suit la première (le Do), il n’y a pas de touche noire entre ces notes. Cette particularité donne à la gamme son nom de diatonique.
-
un intervalle est le nombre de notes entre deux notes sur la gamme diatonique Sur la gamme diatonique de Do, le sol et le DO forment un intervalle de 5 notes nommé quinte, le DO et le MI forment un intervalle de 3 notes nommé tierce.
-
des fonctions parfois données aux notes de la gamme diatonique (en théorie sur la musique tonale) : 1. tonique 2. sus-tonique 3. médiante 4. sous-dominante 5. dominante 6. sus-dominante 7. sensible
-
d’autres gammes peuvent être constituées (une gamme étant un ensemble de notes défini par des intervalles) Cf. autres gammes, plus bas.
-
la tonalité est la première note de la gamme.
-
le mode est la suite des notes de la gamme formée à partir d’une des notes de la gamme.
-
les accords, dans le paragraphe à suivre
Les accords
L’identification des accords se fait sur la gamme diatonique, en donnant un nom à chaque combinaison de notes. La notation d’un accord fonctionne quelque soit la note de départ. L’accord se note avec le numéro de la note (de 1 à 7) dans la gamme. Les numéros au dessus de 7 indiquent les notes de l’octave supérieure (c-a-d la « X » – 7 ème note de l’octave supérieure). Le bémol « b » descend la note d’un demi ton, le dièse « # » la monte d’autant.
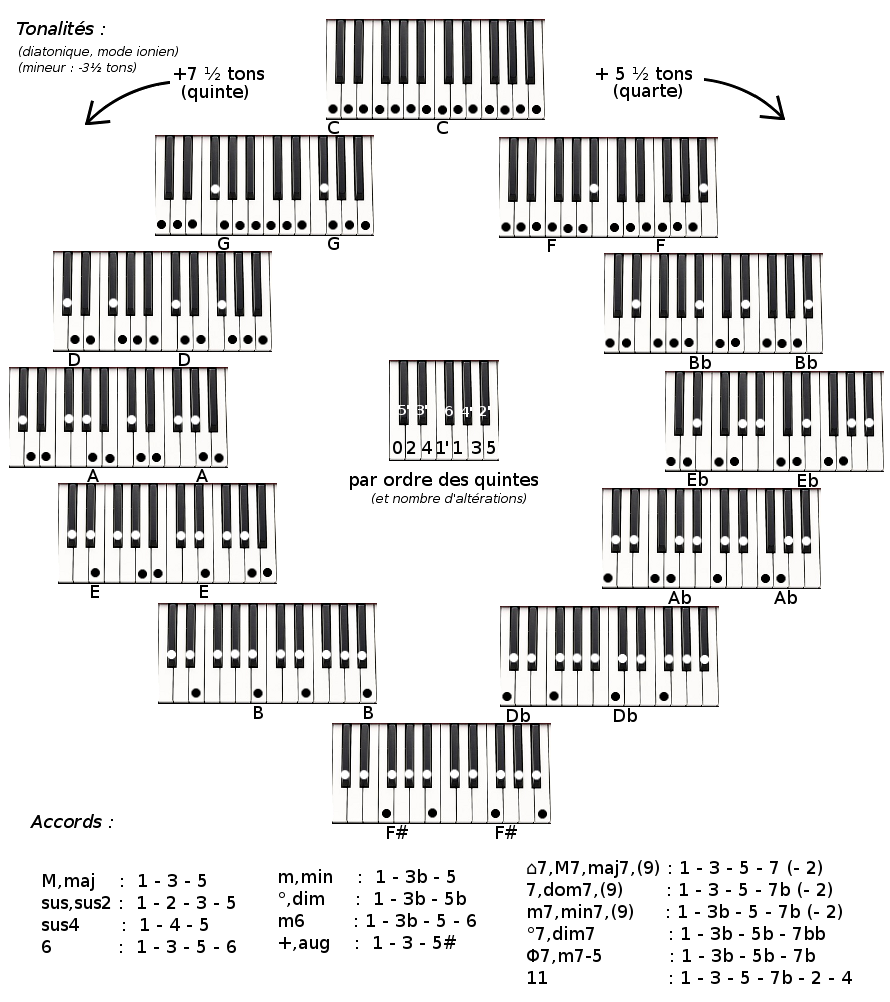
La première carte est maintenant complétée d’accords que nous savons construire à partir de n’importe quelle note, d’après les indications données par la légende, ‘le nom de l’accord’ : ‘les intervalles entre les notes’. L’accord Cm7 par exemple est constitué des notes ‘C,Eb,G,Bb`, car nous prenons la note C suivie des notes ayant pour intervalles 3 bémol, 5 et 7 bémol.
Maîtriser les accords c’est pouvoir jouer rapidement au moins 98,195% ;) des musiques occidentales de toutes les époques, et avoir de bonnes bases pour les autres.
Pour s’entraîner
Voici quelques exemple de repérages dans la carte donnée précédemment.
Rappel : j’ai choisi un morceau que j’aime, j’ai trouvé des notes en essayant de jouer, j’ai écris mes accords, puis j’ai comparé avec la partition d’origine. Mieux que de suivre mes exemples ci-dessous, il est préférable de choisir vos morceaux favoris et de commencer par le plus simple, en suivant la méthode du paragraphe ‘Que faire ?'.
Just The Two Of Us
écrite par Bill Withers, Ralph MacDonald et William Salter.
Le pont (bridge) est constitué des mêmes accords que les parties, mais transposés de 1 ton, 3 fois, avant de retourner à la tonalité d’origine.
(intro,A,B)
DbM7 | Cm7 | Fm7 | Eb7 Ab7
Db: IM7 | viib5 | iii | ii V
Alternative considérant une modulation (les 2 gammes peuvent être utilisées en improvisation) :
Db: IM7 |Eb: vi | ii | Db: ii / V
(bridge)
DbM7 | BbM7 | AM7 | DbM7
Db: IM7 | B:IM7 | A:IM7| Db:IM7
Georgia on my mind
En tonalité Sol (enregistrement de Ray Charles).
Les accords et les degrés sont notés.
Cette musique utilise tous les degrés de la gamme de Sol.
“Modulation relative en Sol” : des modulations sont effectuées entre le mode majeur et mineur de la même tonalité
Impro sur la gamme chromatique : en G éviter C (4th) et F (b7th).
GM7 : en seconde inversion.
G7/D : G7 en seconde inversion.
A7 : en seconde inversion.
AABA
intro:
GM7 | E7 | C7 | C#dim7 | D7
I VI IV bIVdim7| V => I
A:
“Georgia, Georgia ...”
GM7 | B7
I III
"the whole day ..."
Em G7/D | CM7 C#dim7
vi V IV bIVdim7
"Just an old .."
GM7 E9 | A7 D9
I VI ii V
1:
B7 E9 | A7 D7
III VI ii V
2:
GM7 C9 | GM7 B7
I iv I III
B:
“Other arms ...”
Em Am7 | Em6 C9
vi iii vi IV
Em Am7 | Em A7
vi iii vi iii
"still in ..."
Em Am7 | GM7 F#7
vi iii I VII
Bm7 Bb7b5 | A7 D9
iii iii V
Cantaloupe Island
Improvisation modale : cette musique est composée de 3 tonalités. Sur la partie en tonalité Eb, on peut utiliser le mode F dorian pour l’impro. Aussi Ab et Ab blues sont possibles.
(intro)
Eb: Fm7 | % | % | %
ii7
(A)
Eb: Fm7 | % | % | %
ii7
Db: Db7 | % | % | %
I7
C: Dm+4 | % | % | %
ii+4
Eb: Fm7 | % | % | % *2
ii7
(impro)
Ab: vi7 | % | % | %
Gb: vi7 | % | % | %
C: ii+4 | % | % | %
Ab: vi7 | % | % | % *2
Autumn Leaves
La partie A suit le cercle des quartes, et prend un raccourci du degré IV au vii.
L’impro est possible en Bb et sur les ‘blue notes’
(A)
♫ Cm | F ♫ | Bb | Eb
♫ ii | V ♫| I | IV
♫ A0 | D ♫ | Gm | % *2
♫ vii |iii ♫| vi | %
(B)
D | % | Gm | %
iii | % | vi | %
Cm |F9/F7 | Bb | %
ii | V | I | %
(outro)
A | D | Gm | %
vii | iii | vi | %
C/Cm | D | Gm/A0| Gm
ii | iii |vi/vii| vi
The Girl From Ipanema
“Modulation séquentielle” : cette musique a 4 modulations directes en partie B. La même mélodie est jouée sur différentes tonalités, en montant de note, 3 tons de Gb à A, puis 1 demi-ton de A à Bb. L’improvisation peut se faire sur les notes communes aux tonalités.
(Intro)
F: F⌂7 |Gb7+4 *4
I⌂7 |bii7
(A)
F⌂7 | % | G7 | %
I⌂7 | % | ii7 | %
G-7 |Gb7+4| F⌂7 |1:Gb7+4 *2
ii7 |bii7 | I⌂7 | %
(B)
Bg: Gb⌂7| % | B7 | %
I⌂7 | % | IV7 | %
A: F#-7| % | D7 | %
vi7 | % | IV7 | %
Bb: G-7 | % | Eb7 | %
vi7 | % | IV7 | %
F: A-7 | D-7| G-7 | C7
iii | vi | ii | V (turnaround to I)
I Shot The Sherif
La progression d’accords du couplet (verse) est identique à celle trouvée dans “Just the two of us” : “I7, vii0, iii”. Les deux chansons peuvent être jouées sur les mêmes accords. “Just the two of us” a deux accords supplémentaires : “ii, V”. On peut les ajouter à ‘I shot the Sherif’ lorsqu’on la joue en boucle, cela revient à ajouter un rapide “ii V I” appelé ‘turnaround’.
Il est peut-être plus approprié d’utiliser la tonalité mineure relative sur cette musique, parce que la majorité des accords sont mineurs, et parce que la mélodie est plutôt mineure aussi, mais pour l’exercice de cette analyse nous prenons simplement la tonalité relative majeure. Pour rappel, les fonctions harmoniques des degrés i, ii et iii sont équivalentes à celles de I, IV et V. ‘vii’ reste à part.
Le degré vii peut être “demi diminué”, alors noté vii0, ou “quinte diminuée”, alors noté viib5), pour les deux chansons cités.
(chorus)
Eb:
Gm | Gm | Cm | Cm
iii | iii | vi | vi
Gm | Gm | Gm | Gm
iii | iii | iii | iii
(verse)
Eb7 | Dm7 | Gm | Gm | *5
I7 | vii0 | iii| iii |
Gm | Gm | Gm | Gm |
iii | iii | iii| iii|
Killing me softly with his song
Tous les accords correspondent au degrés de la même gamme diatonique majeure, sauf le dernier qui module vers la relative mineure, et l’accord final avec un “majeur VI” (on peut noter que c’est le degré I de la gamme relative mineure. Cette exemple vérifie la règle qui dit que les degrés I IV et V ont les mêmes fonctions que vi ii et iii.
Part A
I heard ... I heard ...
ii7 | V9 | I | IV9
And so ... To listen for a while ...
ii7 | V9 | vi | vi
An there he was ..
ii7 | V7 | I | III7
Part B
Strumming ... Singing ...
vi | ii7 | V | I
Killing me ...
vi | ii | V | IV | I | IV | bvii7 | VI (fine)
Toto – Rosana
Part A "All I wanna do ..."
C: G/2 F: F/2 C C: G/2
V I V V
Part B "Not quite a year since ..."
Bb: Gm/2 F Bb/2 ... Eb/1 Bb/2 F
vi V I IV I V
Chorus : "Meet you all the way ..."
Bb: F Bb/2 Eb/1 ... Eb/1 Bb/2 F
V I IV ... IV I V
Toto – Hold the line
Part A
A: F#m/2 A/1 Bm7 E/2
vi I ii7 V
Part B
Bm7 C#7
ii7 iii7
A-Ha – Take On Me
Intro
A: Bm E/2 A D/2
ii V I IV
Pour aller plus loin
Les progression d’accords
Une gamme est dite harmonisée lorsqu’au moins un accord a été attribué à chacune de ses notes. Chaque accord est appelé un degré, noté I,II,III,IV,V,VI,VII. Lorsque l’on harmonise une gamme diatonique majeure avec des triades, on obtient :
- 3 accords majeurs, les degrés I, IV et V
- 3 accord mineurs, les degrés vi, ii et iii
- 1 accord diminué, le degré VII
Le degré “vi” correspond à la gamme diatonique mineure relative et au mode eolien. Les 2 premières progressions son similaires (même relations), elles couvrent toutes les notes de la gamme et peuvent donc accompagner toute mélodie. ex : on peut faire I-ii-V à la place de I-IV-V (ex: The Beach Boys’ “Good Vibrations).
Il est possible d’harmoniser d’autres gammes : diatonique mineure, diatonique mineure mélodique, diatonique mineure mélodique … avec d’autres accords (en utilisant d’autres notes de la gamme): septième, neuvième …
Chaque accord trouve sa fonction : tension, repos, attraction, distraction, … tonique, dominante, sous-dominante,… Les degrés I,IV et V ont respectivement les fonctions de “Tonique”, “Dominante” et “Sous-dominante” notées “T,S et D”. Les degrés vi,ii et iii ont les mêmes fonctions, notées “t,s et d”.
Un enchainement de degrés dans un gamme est une progression d’accord.
L’utilisation de notes chromatiques (en dehors de la gamme) dans les accords produit une modulation, c-a-d un changement de gamme. On emploi alors le terme de progression de gamme, ou de forme musicale.
Le style, le genre musical
-Reggae :
Les progressions d’accord de base sont I, IV, V, et vi occasionnellement. Exemple : A, D, F#m, E pour I, IV, vi, V. Ils peuvent être ordonnancés à souhait, le début et la fin restant sur I.
Le “reggae bubble” au clavier : sur base 4 temps : 1 – 2 – 3 – 4, main gauche accords sur 2 et 4, main droite accord sur 3 et en fin de phrase accord sur 4.
D’autres gammes
Les intervalles sont donnés en nombre de demis tons.
- orientale
Chaque tetracorde est formé que des groupes de 1/2 tons
2nde augmentés sur chaque tetracorde.
1-3-1 -2- 1-3-1
do réb mi fa sol lab si do
A cause de sa symétrie, le tétracorde supérieur de la gamme
peut constituer le tétracorde d'une même gamme transposée à la dominante :
do réb mi fa sol lab si do
sol lab si do ré mib fab sol
=> Cette gamme évoqué l'Inde.
- hispanique
2-1-2 -2- 2-1-2
do re mib fa sol la sib do
- tzigane
do ré mib fa# sol lab si do
Intervalles : 1 ton - 1/2 ton - 3/2 tons - 1/2 ton - 1/2 ton - 3/2 tons - 1/2 ton
- andalou
do réb mi fa sol lab sib do
1/2 ton - 3/2 tons - 1/2 ton - 1 ton - 1/2 ton - 1 ton - 1 ton
- balkanique
do réb mib fa sol lab si do
1/2ton - 1ton - 1ton - 1ton - 1/2ton - 1ton et demi - 1/2ton
- blues
3, 2, 1, 1, 3, 2
Modes de la gamme diatonique majeure
I ionien C
c-d-e-f-g-a-b
1 - 1 - 1/2 - 1 - 1 - 1 - 1/2
Superman (John Williams)
richesse, optimisme, ouverture
II dorien D
d-e-f-g-a-b-c
1 - 1/2 - 1 - 1 - 1 - 1/2 - 1
médiévale, celtique
III phrygien E
e-f-g-a-b-c-d
1/2 - 1 - 1 - 1 - 1/2 - 1 - 1
Gladiator (Hans Zimmer) :
hispanique
IV lydien F
f-g-a-b-c-d-e
1 - 1 - 1 - 1/2 - 1 - 1 - 1/2
merveilleux, mystère
V mixolydien G
g-a-b-c-d-e-f
1 - 1 - 1/2 - 1 - 1 - 1/2 - 1
The Full Monty (David Lindup)
rock.
VI éolien A
a-b-c-d-e-f-g
1 - 1/2 - 1 - 1 - 1/2 - 1 - 1
36 quai des orfèvres (Erwann Kermorvant) :
gamme mineure naturelle, sombre, mélancolique
VII locrien B
b-c-d-e-f-g-a
1/2 - 1 - 1 - 1/2 - 1 - 1 - 1
?
Remarques sur l’harmonie en fonction du mode
(ionian) I : La 4ème est une note dite 'passing note'
(dorian) ii :
(phrygian) iii : ajouter un 4 diminuée, la 2 et 6 sont des 'passing notes'
(lydian) IV : augmenter la 4 d'un demi ton
(mixolydian) V : La 4ème est une note dite 'passing note'
(aeolian) vi :
(locrian) vii : the 2nde est une 'passing note', et peut être diminuée
